Logaritma

Sifat-Sifat Logaritma

Kita telah mengetahui bahwa fungsi logaritma dengan basis a merupakan fungsi invers dari fungsi eksponensial dengan basis a. Sehingga, logis jika sifat-sifat eksponen berkorespondensi dengan sifat-sifat logaritma. Misalkan, sifat eksponensial a^ua^v = a^{u + v} berkorespondensi dengan sifat logaritma log_a(uv) = log_a u + log_a v.

---

Sifat-Sifat Logaritma
Misalkan a adalah bilangan positif sedemikian sehingga a ≠ 1, dan misalkan n adalah bilangan real. Jika u dan v adalah bilangan real positif, maka sifat-sifat berikut ini benar.

1. log_a(uv) = log_a u + log_a v (Sifat Perkalian)
2. log_a(u/v) = log_a u – log_a v (Sifat Pembagian)
3. log_a uⁿ = n log_a u (Sifat Perpangkatan)

---

Pembuktian Kita menggunakan sifat fungsi invers, yaitu log_a a^x = x.
Sifat 1 Misalkan log_a u = x dan log_a v = y. Jika kita menuliskan bentuk ini ke dalam bentuk eksponensial, kita mendapatkan

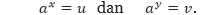
Sehingga,

Sifat 2 Dengan menggunakan Sifat 1, kita peroleh

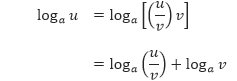
Sehingga,

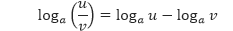
Sifat 3 Misalkan log_a u = x. Maka a^x = u, sehingga

---

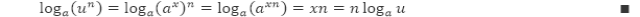
Contoh 1: Menggunakan Sifat-Sifat Logaritma
Tentukan nilai dari masing-masing bentuk berikut ini.

1. log₄ 2 + log₄ 32
2. log₂ 80 – log₂ 5
3. –1/3 log 8

Pembahasan Pertama, kita tentukan nilai log₄ 2 + log₄ 32 seperti berikut.

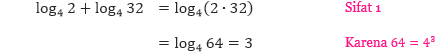
Selanjutnya, kita gunakan Sifat 2 untuk menyelesaikan soal yang kedua.

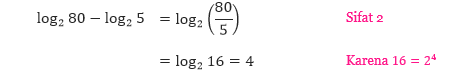
Terakhir, kita gunakan Sifat 3 untuk menentukan nilai bentuk logaritma pada soal ketiga.